Infusion: Internal Diffusion for Video Inpainting

Nicolas Cherel1, Andrés Almansa2, Yann Gousseau1, Alasdair Newson3
1Télécom Paris, 2MAP5, 3Sorbonne Université
arXiv Code Supplementary Data

We propose a diffusion-based video inpainting model. We train our model on a single video relying on the internal content and self-similarity to fill in the masked region. Our approach leverages the diffusion framework which is particularly interesting for dynamic textures but does not require an oversized network.

Abstract

Video inpainting is the task of filling a region in a video in a visually convincing manner. It is very challenging due to the high dimensionality of the data and the temporal consistency required for obtaining convincing results. Recently, diffusion models have shown impressive results in modeling complex data distributions, including images and videos. 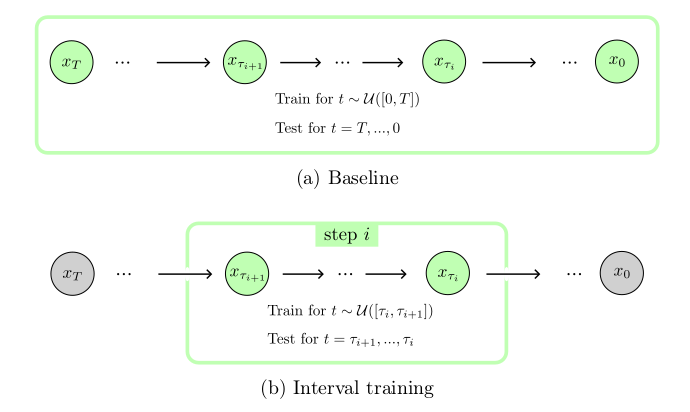Such models remain nonetheless very expensive to train and to perform inference with, which strongly reduce their applicability to videos, and yields unreasonable computational loads. We show that in the case of video inpainting, thanks to the highly auto-similar nature of videos, the training data of a diffusion model can be restricted to the input video and still produce very satisfying results. With this internal learning approach, where the training data is limited to a single video, our lightweight models perform very well with only half a million parameters, in contrast to the very large networks with billions of parameters typically found in the literature. We also introduce a new method for efficient training and inference of diffusion models in the context of internal learning, by splitting the diffusion process into different learning intervals corresponding to different noise levels of the diffusion process. We show qualitative and quantitative results, demonstrating that our method reaches or exceeds state of the art performance in the case of dynamic textures and complex dynamic backgrounds.

Interval training

To improve the results while keeping the network's size relatively small we propose Interval training. We propose to use one lightweight network trained only on a subset of timesteps at a time. We train our model on a given interval. Once training is done on this interval, we use the model to infer the beginning of the next time step. At this point, the model is used for training this next time step. This is carried out until we have reached time step t = 0.

Interval training splits the training of the diffusion model into multiple intervals

Results for texture inpainting with and without interval training

Inpainting results - baseline vs interval training on 2D textures

Results

BibTeX

@misc{cherel2023infusion,
      title={Infusion: Internal Diffusion for Video Inpainting}, 
      author={Nicolas Cherel and Andrés Almansa and Yann Gousseau and Alasdair Newson},
      year={2023},
      eprint={2311.01090},
      archivePrefix={arXiv},
      primaryClass={cs.CV}
}